Exercises

Exercise 11-27

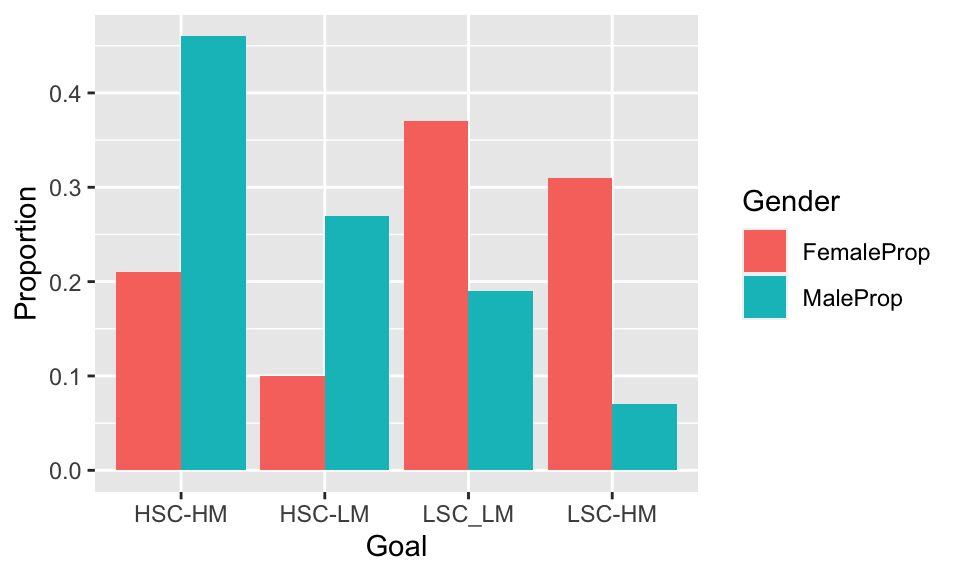
3. There is a remarkable difference in the two distributions. Most of the Male students sports fall in a HSC categories, while most of the female students fall in the LSC categories.

Exercise 11-29 and 11-31

1. H₀: the distribution over the four groups is the same for male and female students at the university of interest
   H_A: the distribution over the four groups is not the same for male and female students at the university of interest

Test to use: \(\chi^2\)-test
Conditions check:
- independent random samples: √, see text - 10% condition; a large university will have more than 670 female and moren than 670 male students
- LC condition, see part (b)

2. Expected Values
   

3. \(\chi^2\) Contributions
   

\(\chi^2\)-value of the test = 24.9 with df = 3.
P-value = 1.622e-05 < .001
P-value < \(\alpha\), so reject H₀.
Context: support found for the hypothesis that the distributions among the four categories differ for male and female students at this university.

Exercise 11-37

2. The null-hypothesis states that all the treatments have the same success rate, even the placebo, for smokers like these in the experiment

3. We use a \(\chi^2\) test for this.

H₀: the success rate is the same for all four treatments
H_A: the success rate is not the same for all four treatments

We use a \(\chi^2\)-test.

Conditions check:
- independent random samples? yes because it is a randomized experiment
- 10% condition; not applicable, because it’s a randomized experiment
- LC condition: all expected values at least 5” yes, see below

Observed Values

Expected Values

\(\chi^2\) Contributions

\(\chi^2\)-value of the test = 34.94 with df = 3.
P-value = 1.256e-07 < .001
P-value < \(\alpha\), so reject H₀.
Context: convincing evidence that at least one of the success proportions for the different treatments, differs significantly from the others.

Exercise 11-39

Follow-up analysis Exercise 11-37
Top 3 ranking of highest contribution to \(\chi^2\)-value:
(1) Successes for treatment 3.Patch plus Drug
(2) Successes for treatment 1.Nicotine Patch
(3) Failures for treatment 3.Patch plus Drug
Treatment 3.Patch plus Drug has the highest positive success rate and lowest failure rate and contributes the most to the \(\chi^2\) test statistic value.
Treatment 1.NicotinePatch has lower success rate than expected, actually comparable with Treatment 4.Placebo.