AP Stats course Teacher: Hans van der Zwan Handout week 48

Literature Starnes D. S., et al. (2015). The Practice of Statistics (5th ed.). New York: W. H. Freeman and Company/BFW.

Handout per lesson

Lesson 1   Sun 2022-11-27

Learning Objectives


No STATS class today


Lesson 2   Mon 2022-11-28

Learning Objectives


Preparation for lesson

See homework previous lesson


Theory

Topics: Random Variables; Expected Value and Standard Deviation Book: pp. 350-355


Class Activities

Lab

  • Exercise 6.5, 6.7, 6.13

Discuss

  • Standard Deviation of Random Variables; book pp. 352-353 and see example below
  • Exercise 17

Expected Value of a Discrete Random Variable The probability distribution of a discrete random variable can be interpreted as ‘expected relative frequencies’ after repeating an experiment many, many times. This does not mean that it is expected to find exactly these probabilities as relative frequencies. It does mean that after repeating the experiment lots of times, the relative frequencies will be close to the probabilities. And according to the law of large number, the more often the experiment is repeated, the closer the experimental relative frequencies are to the probabilities. These expected relative frequencies have an expected mean value associated with them. This expected mean can be calculated as a weighted mean of the possible outcomes with the probabilities as weights. This expected mean value is called ‘the expected value’ of the random variable.

See example on pp. 350-351.

Example What is the expected value of X: the number that comes up when rolling a dice. First construct the probability distribution of X.

x 1 2 3 4 5 6
P(X=x) 1/6 1/6 1/6 1/6 1/6 1/6

Then calculate the Expected Value of X. E(X) = \(\mu_{X}\) = 1.1/6 + 2.1/6 + 3.1/6 + 4.1/6 + 5.1/6 + 6.1/6 = 3 1/2 Note: expected value is not what is expected if a dice is rolled, rolling 3 1/2 is even impossible. Expected value means that if a dice is rolled over en over again, the average value will approach 3 1/2. The more often the dice is rolled, the closer the average is to 3 1/2 (law of large numbers).

Variance and Standard Deviation of a Discrete Random Variable Probability Distributions can be visualized by graphs. Especially histograms are used a lot to visualize them. Based on a histogram, the distribution can be characterized using the SOCS method. The most common way to measure the centre of a probability distribution is by calculating the Expected Value. This is in fact the Mean value of the distribution. To measure the spread, the Standard Deviation (= square root of the Variance), is most commonly used. As with the Expected Value, to calculate the Variance, as in Chapter 1, calculate the average squared distance from the mean. This is the weighted average of the squared distances; the probabilities are the weights to be used. The Standard Deviation is the square root of the Variance. Formulas: \(VAR_X~=~\sum((x_i~-\mu_X)^2~\times~p_i)\) \(SD_X~=~\sqrt{VAR_X}=~\sqrt{\sum((x_i~-\mu_X)^2~\times~p_i)}\)

Example Experiment: rolling two dice S: sum of the two sides coming up The scheme below shows how the Expected Value and the Standard Deviation of S can be calculated. The TI84 can be used to do this as well, see book p. 354.


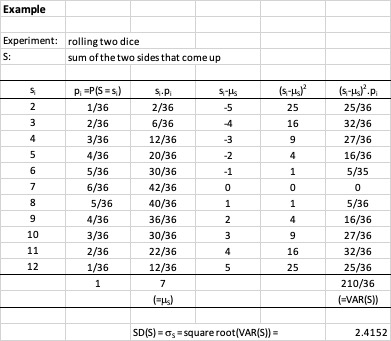
Homework

Study section 6.1. Exercises 6.27 to 6.30

Homework Assigment to hand in

-


Lesson 3   Tue 2022-11-29

Learning Objectives


Preparation for lesson

See homework previous lesson


Theory

Topics: Wrap up Chapter 6 so far; Continuous Random Variables Book: Section 6.1


Class Activities

  • Calculating Expected Value and Standard Deviation with the TI84
  • Continuous Probability Distributions
    • Uniform Distributions
    • Normal Distributions
      • recap; Chapter 2, pp. 108-128
      • Frappy Question on p. 134

Lab

Exercise 2.42, 2.43, 2.53


Homework

Repeat theory about Normal Distributions, pp. 108-128 Exercises 2.42, 2.43, 2.53

Homework Assigment to hand in

-


Lesson 4   Wed 2022-11-30

Learning Objectives


Theory

Topic: Transforming Random Variables Book: pp. 363-368


Preparation for lesson

See homework previous lesson


Class Activities

Discuss

  • Influence of linear transformations on the Expected Value and Standard Deviation of a Random Variable

Rule 1 If X is a discrete random variable and Y = X + c (c a constant), then: \(\mu_Y=\mu_X+c\) and \(\sigma_Y=\sigma_X\) and \(VAR_Y~=~VAR_X\)

Rule 2 If X is a discrete random variable and Y = cX (c a constant), then: \(\mu_Y= c \times \mu_X\) and \(\sigma_Y= c \times \sigma_X\) and \(VAR_Y~=~c^2~\times~VAR_X\)

Rule 3: combining rule 1 and rule 2 If X is a discrete random variable and Y = a + bX (a and b constants), in other words Y is constructed by applying a linear transformation to X, then: \(\mu_Y= a + b \times\mu_X\) and \(\sigma_Y= b \times\sigma_X\) and \(VAR_Y~=~b^2~\times~VAR_X\)

Example The relationship between temperature in \(^0F\) and \(^0C\) is: \(Temperatuur~in~^0F~=~32~+~\frac{9}{5}\times~Temperature~in~^0C\)

Define the random variable T: the maximum temperature in Amman on a randomly chosen day in October in degrees Celsius. Based on historical data, \(\mu_T = 28.6^0C\) and \(\sigma_T = 4.0^0C\). The random variable F is defined as the maximum temperature in Amman on a randomly chosen day in October in degrees Fahrenheit. The question is, what are \(\mu_F\) and \(\sigma_F\)? Applying the rule3: \(\mu_F~=~32~+\frac{9}{5}~\times~\mu_X~=~32~+\frac{9}{5}~\times~28.6~=~83.5~^0F\) \(\sigma_F~=~\frac{9}{5}~\times~\sigma_X~=~\frac{9}{5}~\times~4.0~=~7.2^0F\)

Figure 48.1 Maximum Daily Temperatures in October in Amman, 1979 to 2013

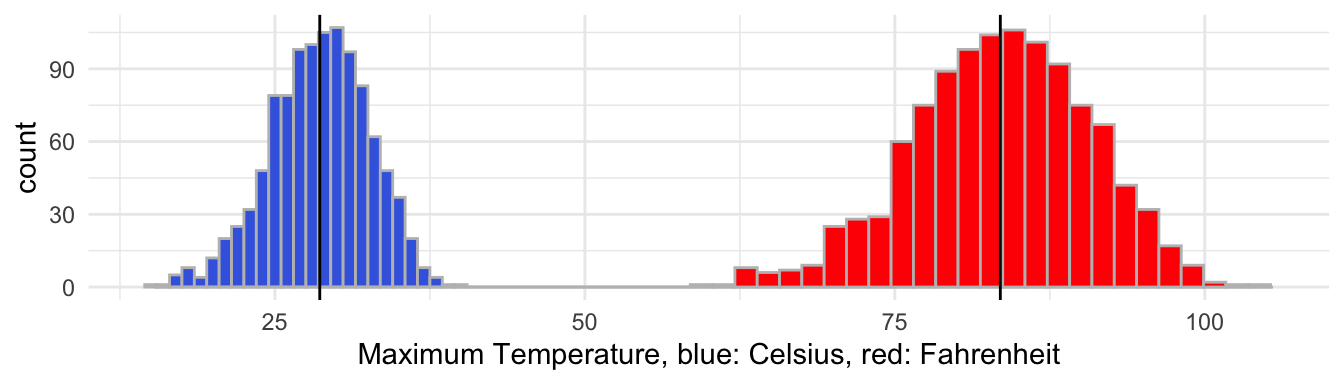
Note. The black lines indicate the mean in \(^0\)C resp. \(^0\)F. As can be seen the average value in \(^0\)F is 32 more than the average in \(^0\)C. The spread of the vales in \(^0\)F is a factor \(\frac{9}{5}\) higher than the spread of the values in \(^0\)C.


Homework

Prepare for test about Chapter 5

Homework Assigment to hand in

-


Lesson 5   Thu 2022-12-01

Learning Objectives


Preparation for lesson

Chapter 5

Class Activities

Test Chapter 5